不确定性与马尔科夫链
文章目录
这个月玩公司的世界杯竞猜游戏,期间经历了各种跌宕起伏,有过竞猜游戏币被清零的记录(后来贷款翻身),也有过“一夜暴富”荣登榜首的时候(多亏了乌拉圭人和巴西人),到现在理论上还保留着拿最后冠军的希望。游戏期间无数次想到了关于“不确定性”的理论,结合以前读书的一些所获,如是有了今天的文字。
一.不确定性
1. 不确定性含义
所谓不确定性,是指超越人类理性驾驭而无法预测的事情。我们生活充满了不确定性。比如:
深圳下半年的房价是会上涨还是下跌?
某互联网公司明年的股票走势如何?
人类的的所有家务劳动,在未来一百年内会不会可以被机器人取代呢?
对于不确定性,其实有两个层面的含义,第一层理解是事物本身不能确定;第二层理解是事物本身是确定的,只是人类无法预知,或者预知要花费的成本不是人类有生之年可以承受的。这两层含义,暂时是无法被证实或证伪的。这就好比如无法证明上帝是否存在一样,但是基督教通过“信仰”来解决,他们告诉你:上帝是存在的,你希望他在他就在,你信他在他就在。
人类对于不确定性有着天生的恐惧,生活在不确定性的世界里的人没有安全感。人类诞生之日起就开始了寻找真理之路。为什么要寻找真理呢?无非就是为自身提供一种安全感。在一个不确定性的世界里,人类不知道自己下一秒自己的命运或财富会不会颠覆,甚至连生命也没法得到保证,所以才会愿意牺牲部分个体活动的自由,集结成群,甚至是让少数人凌驾于自身之上,组织成政府,以取得安全感与保护。
2. 不确定性的根源解释
关于不确定性的根源,哲学与科学上已知的解释有两个:非线性与不确定性原理。
非线性
常见的线性思考:
只要每天多比别人工作2小时,就能产生好的绩效,拿更多的奖金
只要赚到足够的钱,买房买车,心爱的妹子就会嫁给你
经济危机时,只要多发货币就能刺激经济增长(凯恩斯主义)
某公司因为抄袭所以获得了成功
这种简单的“只要…就…”,“因为…所以…“,就是典型的线性逻辑,也是人类大脑天生的默认工作模式,也被称为是一种”思考懒惰“。可是,事物的状态的确定并不是单纯的线性逻辑。多工作两小时,如果工作方向不对,工作方式效率低下,同时身体的精力也是有限,无法长期坚持长时间的工作,能不能产生好的绩效是不确定的;赚到足够的钱,但同时不能忘了,还有很多人跟你一样赚钱买房买车,甚至比你赚的更多,妹子的选择也就更多,最后嫁给你还是嫁给别人也是不确定的。凯恩斯主义就更不用说了,几年前的4万亿产生的后果,你我不都正在尝着吗?某公司抄袭,可是跟它一样抄袭的公司多了去了,最后都剩下的却寥寥无几。
事物的发展按照的是非线性逻辑,决定了事物具有”不确定性“的天然属性。事物初始条件的细微变化都可能引起事物发展方向的极大扭转,以致我们无法预料。如蝴蝶效应,墨菲定律说的就是这个。
不确定性原理
不确定性原理是量子物理学上的一个概念,它表明粒子的位置和动量不可同时被确定。由德国的量子力学奠基人之一维尔纳·海森堡提出,也称为”海森堡不确定性原理“。不确定性原理从量子层面解释了不确定性是物质的固有属性。
通常情况下,不确定性原理易与为大家所熟悉的”观察者效应“所混淆,观察者效应是指被观察的现象会因为观察行为本身而受到一定程度或者很大程度的影响,也就是说由于事物被观察了,从而导致了它的行为路径发生变化。但这两者是不同的,观察者效应强调的是观察本身对事物的发展所产生的影响,而海森堡不确定性原理强调的是事物本身所具有的属性,跟观察本身无关,这点是需要注意的。
前文说到人类对于不确定性有着天生的恐惧,而事物本身具有不确定的天然属性,这里存在着矛盾。而这种矛盾,正是激励人类不断向前追求真理的最大动力。但不管追求真理之路向前走多远,对确定性的知识掌握总是有限,同时,对于一个个体来讲,由于精力和智力所限,能掌握的确定性知识也更为有限。以至于完全靠真理和知识来克服对不确定性的恐惧,是不现实的。为了在真理和知识缺乏的情况下作出准确(或合适)的决策判断,人类学会了概率思考,即从事物的历史发展轨迹中统计分析将来的发展方向。建立了较为完善的数理分析理论,比如提出常见中心极限定理、正态分布、二项式分布等基础的统计知识理论。
在读吴军的《数学之美》一书,对于其中提到的马尔科夫链预测模型印象颇为深刻。马尔科夫链就是一个非常简单的概率思考模型。
二.马尔科夫链
前文说到,随着时间的发展,事物所呈现的状态是不确定的,也可以称为是随机的。比如我们可以将*s1,s2,s3….st,…*看成是这一个月来深圳每天的最高气温,这里的每个*st*都是随机的。同时,事物的每个状态可能与它周围其它的状态相关,比如这一个月每天的最高气温,可能与深圳前段时间的最高气温相关。如果要把每个决定因素考虑进来,将会无比复杂,超出认知预测的范围。为此,俄罗斯数学家安德烈·马尔可夫提出简化的假设:假设事物每个状态,只与它的前一状态相关,而不考虑历史其它状态。比如,我们预测明天的气温,只考虑今天气温,而硬性规定不考虑前天的气温情况。由于,这种状态转换的呈现出链表的形式,所以也称为马尔科夫链。
日常生活中,有很多事情可以用马尔科夫假设来简化的。比如在我们行走时,我们的下一位置,一般只与我们当前的位置(假设为5)有关,我们向前一步,位置就+1(即为6),向后一步位置就-1(即为4),这个下一位置与我们当前位置之前的位置(1,2,3,4)没有关系,可以忽略。当然,并不是每个事物都满足马尔科夫假设,比如彩票。
而将马尔科夫假设与事物状态转换概率结合来就可以建立一个简单的预测模型。我们以天气预测的例子来说明:
根据日常经验,我们看到当前的天气状态是多云时,天气的下一个状态可能会是下雨;而当雨水开始消退,云也减少时,接下来可能就是天晴了。我们收集某个地区十年内的天气数据,计算出每种天气(暂时限制为三种:多云,晴天,雨天)之间相互转化的概率,统计结果如下表:
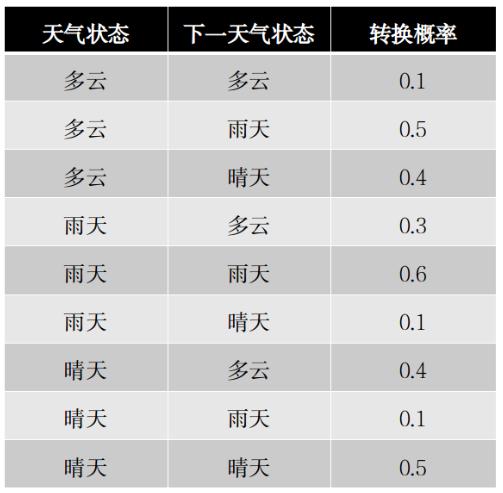
以上转换表可以用状态机来表示:
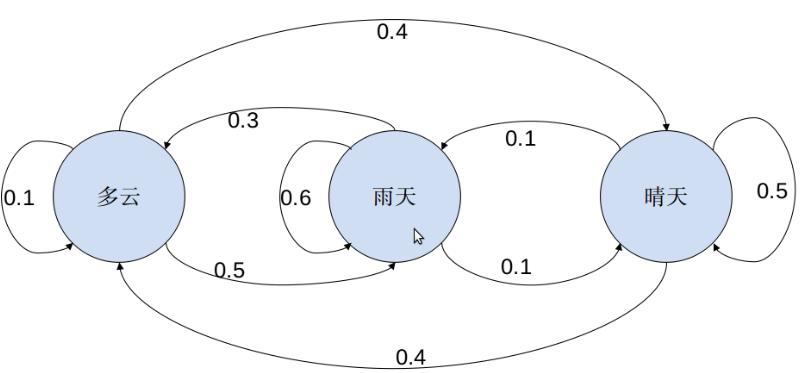
也可以用状态转换矩阵M来表示:
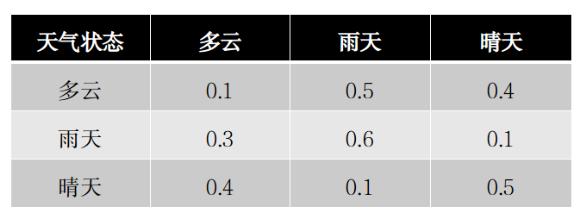
有了状态转换矩阵,通过基本的矩阵运算,就可以对下一天气状态进行预测了。假设当前状态是多云,即100%确认当前天气为多云,可以用向量V来表示:

对下一状态的预测可以通过以下运算求得:
- 下一状态S2 = V×M = [(1 ×0.1 + 0×0.3 + 0×0.4); (1×0.5 + 0×0.6 + 0×0.1); (1×0.4 + 0×0.1 + 0×0.5)] = [0.1; 0.5; 0.4];*
即可得下一状态多云的概率为0.1,雨天的概率为0.5,晴天的概率为0.4,雨天的可能性最大
继续计算下一状态S3
*S3 = S2×M =[(0.1×0.1 + 0.5×0.3 + 0.4×0.4); (0.1×0.5 + 0.5×0.6 + 0.4×0.1); (0.1×0.4 + 0.5×0.1 + 0.4×0.5)] = [0.32; 0.39; 0.29];*
不出意料,雨天的可能性还是最大。无论再计算多少步,结果都会是雨天的可能性最大。这是为什么呢?是因为状态转换表只保存了最后的一个状态的信息,所有的状态转换只与最后一个状态信息相关,所以,接下来的状态也就逃脱不出初始状态的约束了。这种只考虑最后一个状态信息的马尔科夫链称为1阶马尔科夫链。那如如果要提高准确性,使得下一状态不只是受上一状态的约束,该怎么做呢?可能你已经想到了,提升到多阶马尔科夫链*即可。比如2阶马尔科夫链的转换概率表可以用如下的表格来表示(只画出了1/3部分,其它部分依次类推,共会有18种组合):
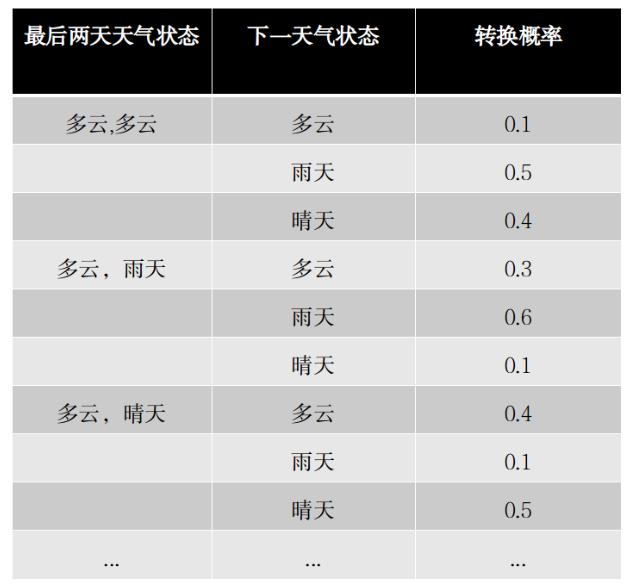
以上2阶状态转换表,表明了下一天气状态是由最后两天的天气决定,由它计算出来的结果准确性会比1阶的矩阵计算结果要高,随着阶数的继续递增,准确性也会相应的提高。可是这个提高是有代价的,阶数越高,计算的复杂性也就越大,而且是呈指数级的增长而非线性的增长。当阶数增大一定程度,计算的复杂度超过人类现有的计算能力范围后,问题也就变成了不确定性问题了。
总结:
世界万物具有本质的不确定性,人类由于对不确定性的恐惧而选择追逐真理。但是,完全靠真理来克服对不确定性的恐惧是不现实的,有时候我们需要学会接受不确定性,并通过概率思考来来对不确定性作出决策判断。马尔科夫链模型就是一个非常简单的概率决策模型,是很好的概率思考实践。
最后PS一条:如果你没法掌握足够的股票市场一手信息,遵循“买涨不买跌”的原则进行股票交易的话,会比你无意义的各种推测要好的多!
文章作者 justin huang
上次更新 2014-07-13